Zadání
- Naprogramujte řešení 0/1 problému batohu hrubou silou. Na zkušebních datech pozorujte závislost výpočetního času na n.
- Naprogramujte řešení 0/1 problému batohu heuristikou podle poměru cena/váha. Pozorujte
- závislost výpočetního času na n. Grafy jsou vítány (i pro exaktní metodu).
- průměrné zhoršení proti exaktní metodě
- maximální relativní chybu. Absolutní chyba nic neříká!
Definice problému
- Je dáno:
- celé číslo n (počet věcí)
- celé číslo M (kapacita batohu)
- konečná množina V={v1, v2, ... ,vn } (hmotnosti věcí)
- konečná množina C={c1, c2, ... ,cn } (ceny věcí)
- Zkonstruujte množinu X={x1, x2, ... ,xn }, kde každé xi je 0 nebo 1, tak, aby
- platilo: v1x1+v2x2 + ... + vnxn <= M (batoh nebyl přetížen).
- výraz c1x1+c2x2 + ... + cnxn nabýval maximální hodnoty pro všechny takové množiny (cena věcí v batohu byla maximální).
Implementace
Úlohu jsem implementoval v Jazyce C# jako konzolovou aplikaci. Data načítá ze standardního vstup a výsledky vypisuje na stdandardní výstup. Řešení jsem rozdělil do 4 tříd.- Batoh.cs - Virtuální třída, má implementované metody pro načítání ze standardního vstupu, výpis na standardní výstup a virtuální metodu Compute().
- BruteForce.cs - Řešení hrubou silou, implementováno rekurzivně.
- GreedyProof.cs - Jednoduchá heuristika, nejprve vypočte poměr cena/váha a nastaví pomocné pole s indexy, které představují pořadí ve kterém budou prvky do batohu přidávány (od nejlepšího poměru).
- Program.cs - Načte vstupní data a volá metodu Compute() a měří čas.
Parametry programu
- -g jednoduchá heuristika (GreedyProof), jinak hrubá síla (BruteForce).
- -t:count Pro měření času, každou instanci opakuje count-krát.
Naměřené hodnoty a výsledky
Měřil jsem na NTB s procesorem Centino 1.4GHz, nastavení max Performance při napájení z adaptéru. Použitý OS: Windows XP SP2 s .net Framework 2.
Tabulka výsledků měření
Protože rozlišení čítače (Environment.TickCount) je 16 ms, je nutné instance spočítat vícekrát a výsledný čas získat vydělením počtem opakování. Pro měření časové složitosti hrubé síly jsem experimentálně nastavoval počet opakovaní od 100 000 (pro n = 4) do 1 (pro n = 30). Pro měření heuristiky jsem nastavil 100 000 opakování pro každou instanci problému.
| n | hrubá síla [ms] | heuristika [ms] | IDmax. chyby | prum. zhoršení | max. chyba |
|---|---|---|---|---|---|
| 4 | 0,0075 | 0,0071 | 9037 | 2,17% | 36,36% |
| 10 | 0,044 | 0,015 | 9080 | 1,73% | 11,48% |
| 15 | 1,229 | 0,021 | 9126 | 1,32% | 8,54% |
| 20 | 36,865 | 0,027 | 9165 | 1,14% | 8,43% |
| 22 | 136,736 | 0,030 | 9237 | 1,05% | 7,23% |
| 25 | 1140,04 | 0,034 | 9283 | 0,96% | 3,68% |
| 27 | 4803,9 | 0,036 | 9338 | 0,90% | 10,60% |
| 30 | 38723,1 | 0,041 | 9380 | 0,85% | 5,51% |
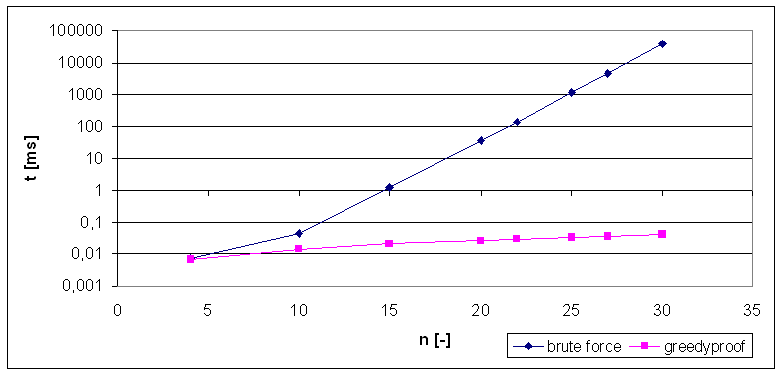
Graf: Časová závislost
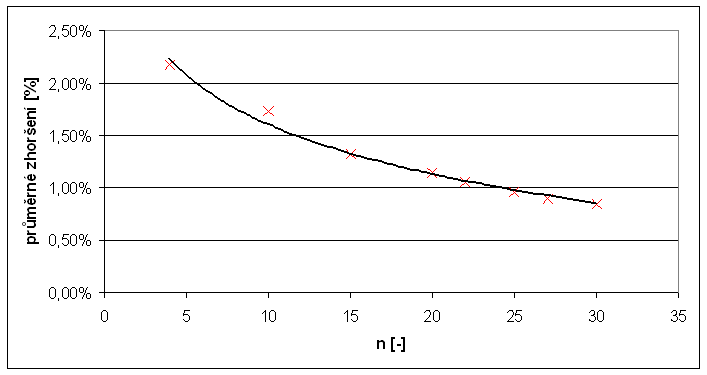
Graf: Závislost průměrné chyby na velikosti instance
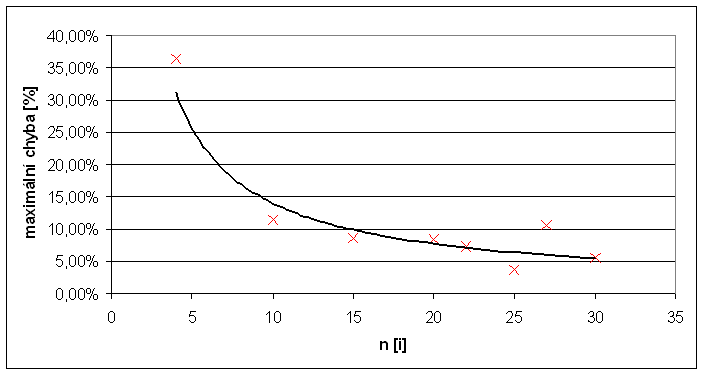
Graf: Závislost maximální chyby na velikosti instance
Závěr
Řešení hrubou silou dává sice nejlepší možné řešení, ale daní za prohledání celého stavového prostoru je neúnosná (exponenciální) časová složitost. Překvapující jsou poměrně dobré výsledky jednoduché heuristiky. Časová závislost je lineární (obsahuje velkou multiplikativní konstantu, takže pro malá n se neprojeví složitost řazení n.log(n)) a dosahuje průměrné chyby v nejhorším případě 2,17% pro zadané instance. Z grafu je dobře patrné, že průměrná relativní chyba s velikostí instance klesá.