Zadání
- Naprogramujte řešení 0/1 problému batohu metodou větví a hranic (B&B) tak, aby omezujícím faktorem byla hodnota optimalizačního kritéria. Tj. použijte ořezávání shora (překročení kapacity batohu) i zdola (stávající řešení nemůže být lepší než nejlepší dosud nalezené)
- Naprogramujte řešení 0/1 problému batohu nebo alespoň 0/1 exaktního problému batohu bez cen metodou dynamického programování.
- Naprogramujte řešení 0/1 problému batohu heuristikou podle poměru cena/hmotnost s testem nejcennější věci.
Definice problému
- Je dáno:
- celé číslo n (počet věcí)
- celé číslo M (kapacita batohu)
- konečná množina V={v1, v2, ... ,vn} (hmotnosti věcí)
- konečná množina C={c1, c2, ... ,cn} (ceny věcí)
- Zkonstruujte množinu X={x1, x2, ... ,xn}, kde každé xi je 0 nebo 1, tak, aby
- platilo: v1x1+v2x2 + ... + vnxn <= M (batoh nebyl přetížen).
- výraz c1x1+c2x2 + ... + cnxn nabýval maximální hodnoty pro všechny takové množiny (cena věcí v batohu byla maximální).
Implementace
Úlohu jsem implementoval v Jazyce C# jako konzolovou aplikaci. Název souboru se vstupními daty je první argument a je povinný. Druhý argument je nepovinný a udává počet opakování výpočtu jedné instance (Důležité pouze při měření času).Maximálně jsem recykloval úlohu "batoh 1" (virtuální třída batoh a třídu program, kde je implementováno měření času)
- Batoh.cs - Virtuální třída, má implementovanou metody pro čtení vstupního souboru a virtuální metodu Compute().
- Program.cs - Volá metodu Compute() a měří čas.
- GreedyProofMod.cs - Kombinovaná heuristika, rozšíření jednoduché heuristiky (batoh 1) o test nejcennější věci. Naleznu nejcennější věc a pokud je její cena lepší než výsledek jednoduché heuristiky (GreedyProof) označím ji za výsledek.
- Dyn.cs - Dynamické programování dekompozicí podle kapacity batohu. (algoritmus pro vyplnění 2D pole - slide cv.3)
- BB.cs - Metoda větví a hranic. Vychází z BruteForce - DFS (batoh 1), které je implementováno rekurzivně s ořezáváním nepřípustných stavů (překročení kapacity batohu). Je přidáno ořezání neperspektivních stavů po nalezení řešení (pokud expandováním současného stavu nemůžu dostat lepší řešení, než které je nalezeno, tento stav dále neexpanduji)
Naměřené hodnoty a výsledky
Měřil jsem na NTB s procesorem Centino 1.4GHz, nastavení max Performance při napájení z adaptéru. Použitý OS: Windows XP SP2 s .net Framework 2.
Tabulka: Srovnání výpočetních časů
Protože rozlišení čítače (Environment.TickCount) je 16 ms, je nutné instance spočítat vícekrát a výsledný čas získat vydělením počtem opakování. Počet opakování jsem nastavoval experimentálně, tak aby bylo rozlišení času dostatečné).
| n | hrubá síla [ms] | heuristika [ms] | kombinovaná heuristika [ms] | Dynamické programování [ms] | B&B [ms] |
|---|---|---|---|---|---|
| 4 | 0,008 | 0,007 | 0,007 | 0,027 | 0,007 |
| 10 | 0,044 | 0,015 | 0,014 | 0,063 | 0,033 |
| 15 | 1,230 | 0,021 | 0,020 | 0,168 | 0,13 |
| 20 | 36,87 | 0,027 | 0,026 | 0,268 | 3,43 |
| 22 | 136,74 | 0,030 | 0,030 | 0,292 | 14,24 |
| 25 | 1140,04 | 0,034 | 0,035 | 0,393 | 101,33 |
| 27 | 4803,90 | 0,036 | 0,036 | 0,490 | 400,76 |
| 30 | 38723,10 | 0,041 | 0,039 | 0,626 | 3371,26 |
Tabulka: Průměrná chyba heuristik
| n | 4 | 10 | 15 | 20 | 22 | 25 | 27 | 30 |
|---|---|---|---|---|---|---|---|---|
| jednoduchá heuristika | 2,17% | 1,29% | 0,48% | 0,60% | 0,69% | 0,50% | 0,50% | 0,49% |
| kombinovaná heuristika | 1,33% | 1,10% | 0,31% | 0,43% | 0,54% | 0,42% | 0,29% | 0,38% |
Tabulka: Maximální chyba heuristik
| n | 4 | 10 | 15 | 20 | 22 | 25 | 27 | 30 |
|---|---|---|---|---|---|---|---|---|
| jednoduchá heuristika | 36,36% | 11,48% | 8,54% | 8,43% | 7,23% | 3,68% | 10,60% | 5,51% |
| kombinovaná heuristika | 24,75% | 11,48% | 2,77% | 4,08% | 3,02% | 2,59% | 1,85% | 1,75% |
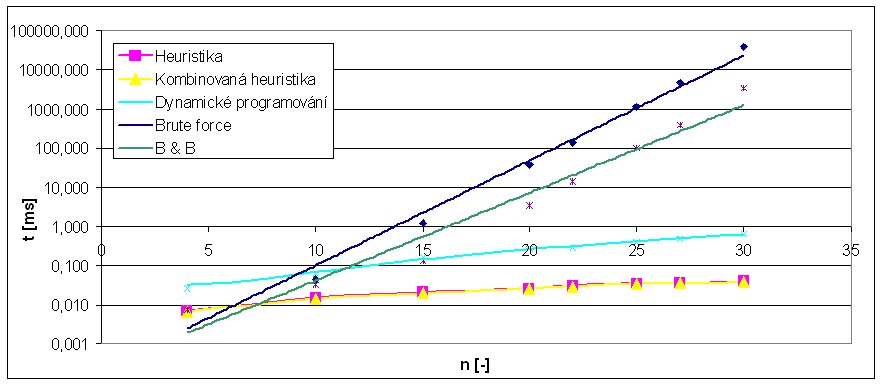
Graf: Časová závislost
Graf: Závislost průměrné chyby na velikosti instance
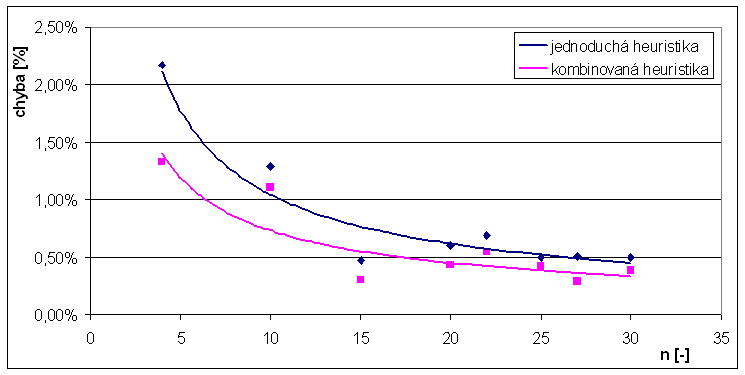
Graf: Závislost maximální chyby na velikosti instance
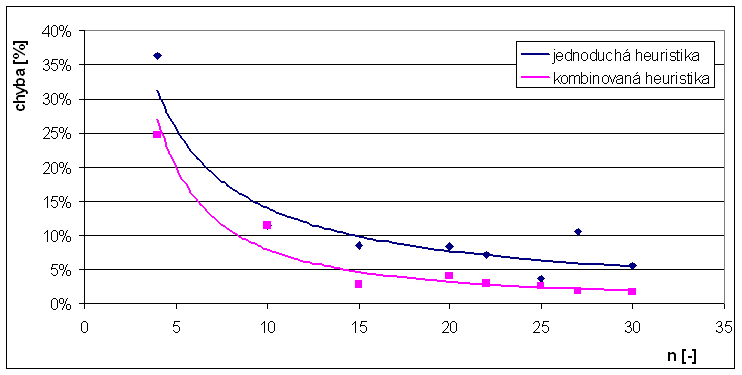
Závěr
Oproti "jednoduchým" metodám řešení, použitých v úloze batoh 1, je z grafů dobře patrné velké snížení časové náročnosti. Metoda větví a hranic (B&B) přináší zlepšení o jeden řád oproti DFS. Přitom se jedná o přidání jedné podmínky.
Ještě mnohem lepších výsledků dosahuje metoda dynamického programovaní. Sice v porovnání s heuristikou (greedyProof) je o řád pomalejší, ale oproti ní poskytuje vždy optimální řešení. Pouze si musíme uvědomit paměťovou složitost, která je dána 2D polem, v tomto případě M.n. Přidáním testu nejcennější věci do heuristiky se snížila průměrná a maximální chyba.